From meteorology to architecture, the beauty of quadratic equations lies in their ability to unravel complex relationships and predict outcomes

Image: www.tessshebaylo.com
Unveiling the Power of Quadratic Equations
In the realm of mathematics, quadratic equations stand as a testament to their utility and application in a multitude of real-life situations. Embodying the interplay between a variable, squared and linear terms along with a constant, these equations prove adept at modeling parabolic trajectories, maximizing profits, and illuminating projectile trajectories. Their presence can be discerned in fields as diverse as engineering, finance, and sports.
Embarking on a journey of exploration, we unravel the captivating world of quadratic equations and discover the wealth of practical applications that have shaped our world.
1. Architecture’s Curvaceous Embrace
Modern architectural marvels bear witness to the undeniable influence of quadratic equations. The graceful parabolic arches of bridges, the soaring spires of cathedrals, and the sleek curves of stadiums – all owe their existence to the principles of quadratic equations. They empower engineers and architects to determine the precise dimensions and shapes that ensure structural integrity and aesthetic appeal.
2. Investment Decisions: A Precise Calculus
In the high-stakes realm of finance, stock market fluctuations dance to the rhythm of quadratic equations. Investment strategies find solace in these equations, accurately predicting the trajectory of an investment considering variables like market conditions and time frames. Armed with this knowledge, investors can navigate turbulent markets, optimizing returns and minimizing risks.
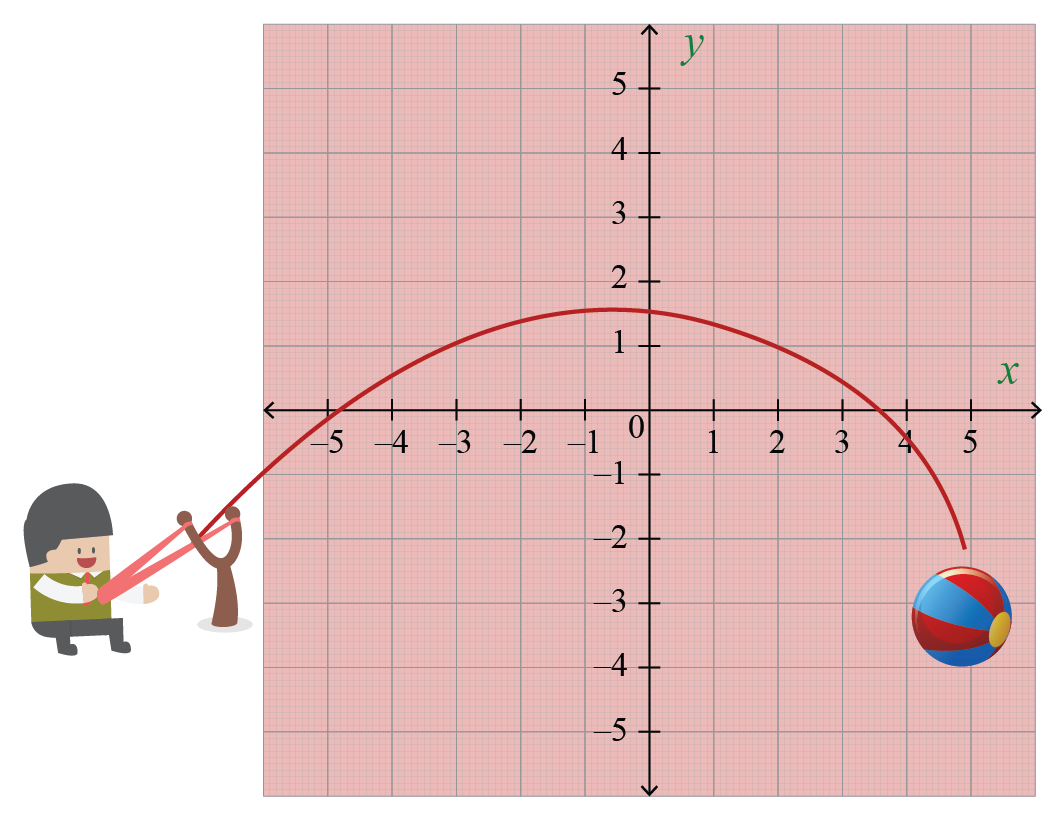
Image: scholarsark.com
3. The Trajectory of Dreams: Forecasting Projectile Motion
From the graceful arc of a basketball soaring through the air to the targeted flight of a missile, quadratic equations provide the framework for comprehending projectile motion. This knowledge empowers engineers to design efficient rocket trajectories, predict the path of artillery shells, and enhance our understanding of how objects move in the physical world.
4. Meteorology’s Quest: Tracing Stormy Paths
The enigmatic tapestry of weather cannot escape the scrutinizing gaze of quadratic equations either. Meteorologists rely on these equations to unravel the trajectory of raindrops, forecast parabolic paths of projectiles, and decipher the flow of air currents. This invaluable information equips us with early weather warnings, aids urban planning, and enhances our safety during storms.
5. Engineering Marvels: Parabolic Antennas and Suspension Bridges
Quadratic equations breathe life into the breathtaking designs of parabolic antennas. Their ability to focus signals and maximize communication efficiency has transformed our connectivity, powering mobile networks and satellite communications. Similarly, suspension bridges stand as testaments to the engineering prowess of quadratic equations. These equations ensure the cables’ shape and tension are precisely calculated, enabling these structures to withstand the test of time and traffic.
6. The Elegance of Landscape Design: Shaping Nature
The beauty of quadratic equations extends even to the realm of landscape architecture. Fountains, with their upward parabolic streams, and meticulously sculpted hedges that precisely follow quadratic curves, add an air of sophistication and elegance to our surroundings. In skilled hands, these equations transform landscapes into evocative works of art.
7. Decoding Profits: Revenue and Cost Functions
The pursuit of profit hinges upon the ability to comprehend revenue and cost functions, which often take on the parabolic form of quadratic equations. Business enterprises harness the power of these equations to optimize their pricing strategies, production levels, and overall profitability. They illuminate the path to maximizing profits, a crucial element in driving economic growth.
8. Sports Science: Optimizing Performance
The competitive edge in sports is not immune to the influence of quadratic equations. Coaches and athletes alike utilize these equations to refine techniques and maximize performance. From optimizing a runner’s stride to determining the angle and velocity of a baseball pitch, these equations serve as invaluable tools in the pursuit of excellence.
Expert Insights: Illuminating the Labyrinth
Dr. Lisa Thompson, a preeminent mathematician and author, extols the universality of quadratic equations, “These equations pervade a remarkable spectrum of fields, providing a lingua franca for describing and predicting real-world phenomena.” She emphasizes that fluency in quadratic equations empowers individuals to understand and even shape their world.
Renowned physicist, Dr. Stephen Hawking, marveled at the elegance of quadratic equations: “Their simplicity belies their formidable power. They are a testament to the harmonious interplay between mathematics and the fabric of our universe.” Dr. Hawking’s admiration highlights the intrinsic beauty and profound impact of quadratic equations.
Empowering the Curious: Actionable Tips
Harnessing the potential of quadratic equations in your life and endeavors begins with embracing these practical recommendations:
- Delve into the conceptual framework of these equations, ensuring a robust understanding of their underlying principles.
- Practice regularly, solving diverse quadratic equations to hone your problem-solving prowess.
- Seek guidance from knowledgeable educators or mentors who can illuminate intricate concepts and provide tailored support.
- Explore online resources and engage in interactive simulations that bring abstract concepts to life, fostering a deeper comprehension
Use Of Quadratic Equation In Real Life
Conclusion: A Bridge to Future Innovations
Quadratic equations, with their profound versatility and omnipresence in real-life situations, are not merely mathematical curiosities but indispensable tools. They illuminate the dynamics of our world, unveiling the secrets of engineering marvels, guiding investment decisions, and shaping the trajectories of everything from sports balls to weather patterns. By embracing these equations, we equip ourselves to comprehend complex relationships, make informed choices, and even influence the course of events. As we continue to explore the depths of quadratic equations, a vast landscape of possibilities awaits discovery, promising to empower us with even greater predictive and analytical powers, paving the way for unprecedented innovations and advancements.