In the realm of numbers, prime numbers stand apart as the enigmatic building blocks of all others. Their allure stems from their elusive nature, appearing sporadically among the vast sea of integers. 13, an age-old object of curiosity, presents an intriguing question: does it belong to the elite league of prime numbers or fall into the realm of composite numbers? Join us on an explorative journey to decipher the number 13’s true identity.

Image: mavink.com

Defining the Prime-Composite Divide

The pivotal distinction between prime and composite numbers hinges on their divisibility characteristics. Prime numbers are defined as the positive integers greater than 1 that possess precisely two positive divisors: themselves and 1. Composite numbers, on the other hand, are those greater than 1 that have more than two divisors. Understanding this fundamental distinction sets the stage for our investigation of the number 13.

Examining the Divisor of 13

Embarking on a methodical analysis, let’s determine 13’s divisors. A number is prime if it has no divisors other than itself and 1. Beginning with the first positive integer, 1 divides 13 evenly. Trying 2, we find it doesn’t divide 13. Moving on to 3, we again find no clean division. This process continues until we reach 12, which divides 13 without leaving a remainder. Crucially, as 12 is not equal to 1 or 13, it establishes 13 as a composite number.

Exploring the Properties of Composite Numbers

Composite numbers, a class that encompasses the majority of integers, invite further scrutiny. They are akin to mosaics, composed of the multiplication of two or more prime numbers. This intricate composition influences their behavior in various mathematical operations. Composite numbers bear traits that distinguish them from their prime counterparts, enriching our understanding of numerical relationships.

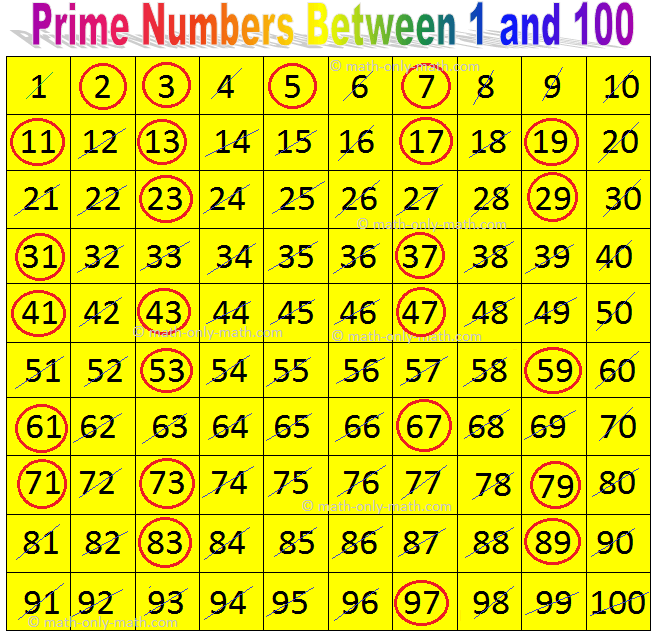
Image: www.animalia-life.club

Significance in Prime Number Theory

Despite not being prime, 13 occupies a prominent place in prime number theory. Prime constellations, such as the Fibonacci sequence and twin primes, often exhibit patterns involving 13. Its odd nature and proximity to the prime number 11 make it an intriguing subject of study for number theorists. The ongoing pursuit of understanding these connections深ens our knowledge of the distribution and behavior of prime numbers.

Is 13 A Prime Number Or A Composite Number

Conclusion

Our investigation has determined that 13 is indeed a composite number, composed of the factors 1 and 13. Even though it falls short of prime status, 13’s unique characteristics and its significant presence in prime number theory and beyond continue to intrigue researchers and mathematicians. The blend of prime and composite numbers enriches the fabric of mathematics, providing a tapestry of numerical beauty for our contemplation and admiration.