In the realm of fractions, the question of whether 1/4 is bigger than 1/2 might seem counterintuitive at first glance. To untrained eyes, 4 might appear to be a larger number than 2, prompting the assumption that 1/4 could potentially outweigh 1/2. However, a closer examination reveals that this is not the case, and 1/2 is indeed the greater of the two fractions.
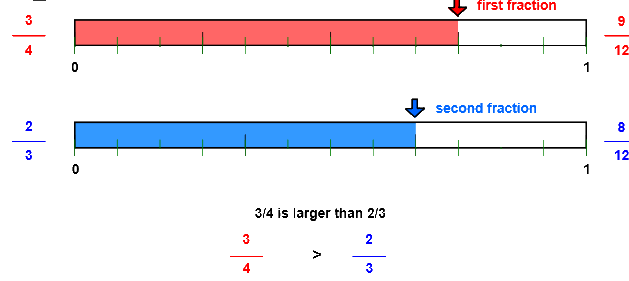
Image: en.asriportal.com
To delve into the logic behind this conclusion, it’s imperative to revisit the fundamental concept of fractions. In essence, fractions represent parts of a whole, wherein the numerator signifies the number of equal parts being considered, and the denominator denotes the total number of equal parts that constitute the whole.
A Closer Look at 1/4 and 1/2
With this understanding in mind, let’s scrutinize 1/4 and 1/2 more closely. In 1/4, the numerator 1 indicates that we’re dealing with one part out of the total of four equal parts. In 1/2, on the other hand, the numerator 1 represents one part, but this time, out of a total of two equal parts.
Now, envision a visual representation of these fractions. Think of them as parts of a pizza, neatly sliced into equal-sized pieces. If the pizza is divided into four slices, 1/4 would represent a single slice out of the four. Conversely, if it’s cut into two equal halves, 1/2 would be one out of those two halves.
Determining the Greater Fraction
To determine which fraction is larger, it’s crucial to compare their proportional sizes relative to the whole. Since 1/4 represents one out of four equal parts, and 1/2 represents one out of two equal parts, it becomes evident that 1/2 claims a larger portion of the whole compared to 1/4.
This can also be mathematically demonstrated by converting both fractions into decimal form. 1/4 can be expressed as 0.25, and 1/2 translates to 0.5. Evidently, 0.5 is a greater value than 0.25, further corroborating the conclusion that 1/2 surpasses 1/4 in terms of magnitude.
Latest Trends and Developments
In the ever-evolving realm of mathematics, scholars and educators are continuously exploring innovative methods to enhance the comprehension of fractions. Some recent trends include:
- Visual representations: Capitalizing on the power of visualization, teachers employ diagrams, models, and hands-on activities to make abstract concepts like fractions more tangible and relatable.
- Fraction manipulatives: These physical tools, such as fraction circles or bars, enable students to visualize and manipulate fraction values, fostering a deeper understanding of comparative sizes and operations.
- Fraction number lines: This visualization tool helps learners compare and order fractions by representing them on a number line, making it easier to grasp their relative magnitudes.
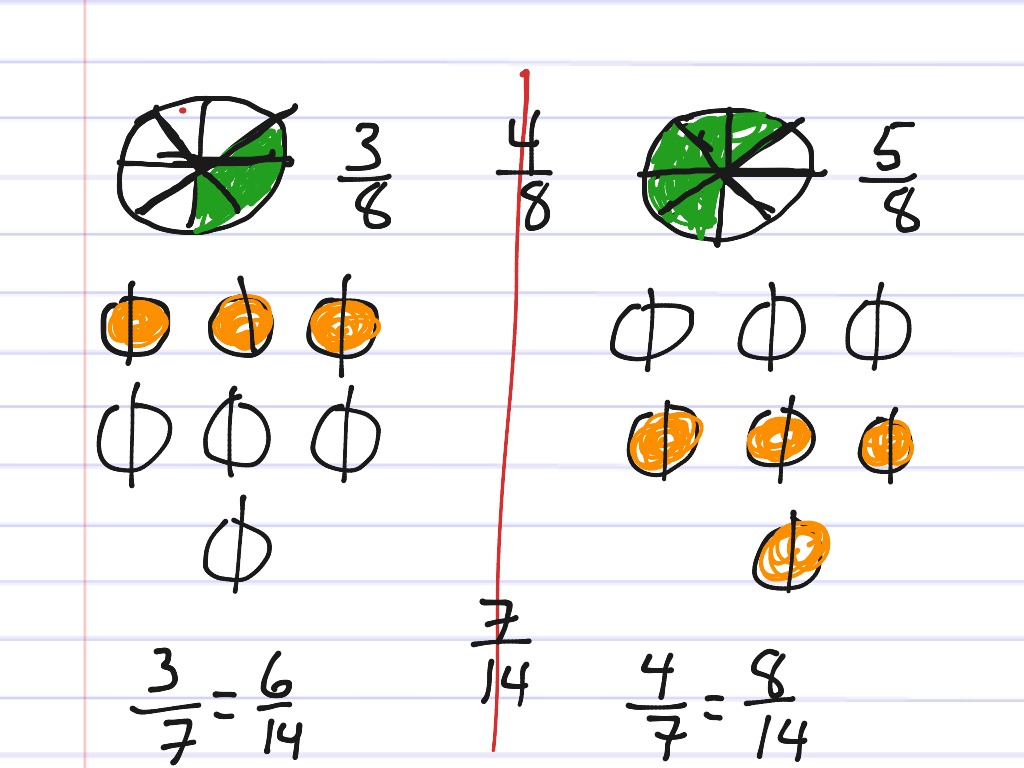
Image: www.showme.com
Tips for Grasping Fraction Concepts
Understanding fractions can be a rewarding endeavor when equipped with effective strategies. Here are a few tips to help you master this numerical realm:
- Visualize, visualize, visualize: Convert abstract fraction concepts into visual representations to aid your comprehension. Draw diagrams, use fraction models, or engage in hands-on activities.
- Compare and contrast: Juxtapose different fractions by converting them into decimals or using visual aids to discern their relative sizes and relationships.
- Practice regularly: Proficiency in fractions requires consistent practice. Engage in exercises, solve fraction problems, and explore various fraction manipulatives to reinforce your understanding.
Frequently Asked Questions
Here are some commonly asked questions regarding fractions, along with clear and concise answers to help you navigate this mathematical terrain:
How do I convert a fraction to a decimal?
How do I compare fractions with different denominators?
How can I learn fractions effectively?
Is 1 4 Bigger Than 1 2
Conclusion
In addressing the question “Is 1/4 bigger than 1/2?”, we’ve unveiled that 1/2 indeed holds the upper hand. By deconstructing fractions into their constituent parts and visualizing them, we’ve gained a clear understanding of their relative magnitudes.
If you’re eager to delve deeper into the enchanting world of fractions, I encourage you to explore the resources and tips shared within this article. With perseverance and a touch of mathematical curiosity, you’ll undoubtedly conquer the intricacies of fractions and unlock their endless applications!