Welcome, curious minds! Today, we embark on an exciting expedition to unravel the secrets of polygons and discover the formula to calculate their perimeter. Our adventure begins by delving into their alluring world, where familiarity breeds understanding and knowledge empowers problem-solving. Get ready to join the ranks of geometry enthusiasts as we conquer the enigma of finding the perimeter of polygons with aplomb!
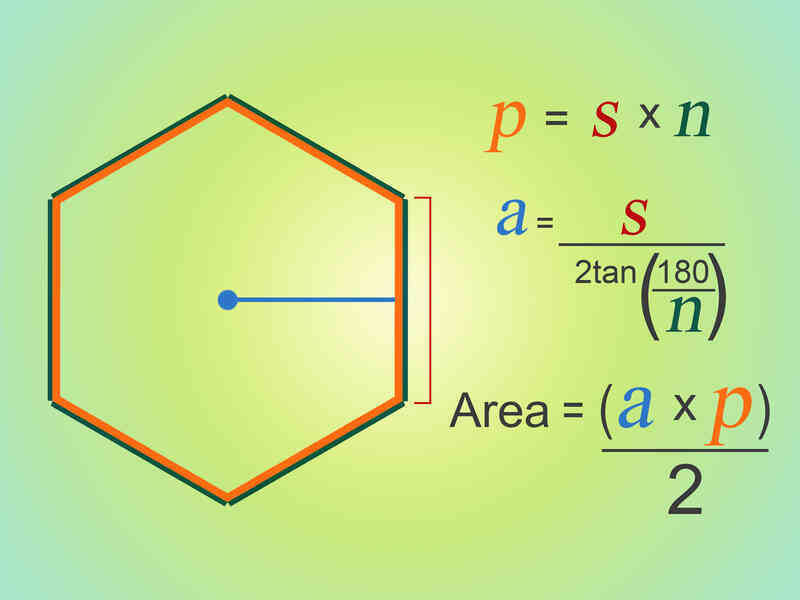
Image: www.consejosytrucos.net
Defining Polygons: Unveiling Their Nature
Polygons, geometrical marvels, grace our world in diverse forms, from the unassuming triangle to the intricate sunflower. United by their defining characteristic—straight sides—these figures captivate our curiosity. Imagine a mosaic of polygons adorning a dazzling stained-glass window, each piece adding beauty and complexity to the composition. Their practical applications abound, from architecture’s grand structures to engineering’s precision designs. Understanding polygons is a cornerstone in the domain of geometry, empowering us to unlock their mysteries.
Formula Unraveled: The Secrets of Perimeter Unlocked
To unravel the enigma of polygon perimeter, we invoke the formula: Perimeter = Sum of side lengths. Just as a fence encloses a garden, the perimeter embraces the polygon, outlining its boundaries and defining its size. Envision a polygon as a stage, with each side representing an act in a captivating play. The perimeter, then, becomes the grand curtain call, encompassing all the facets of the polygon’s journey.
Dissecting Polygons: Uniting Theory and Practice
To solidify our comprehension, let’s dissect a triangle, the simplest of polygons. Armed with a ruler, we measure its three sides: 5 cm, 7 cm, and 9 cm. Uniting the theory and practice, we forge ahead and calculate the perimeter. Perimeter = Sum of side lengths = 5 cm + 7 cm + 9 cm = 21 cm. Eureka! We have conquered the triangle, unveiling its perimeter.

Image: classcampusbrandt.z19.web.core.windows.net
Generalizing the Formula: Unifying Irregular Shapes
Expanding our horizons beyond triangles, we venture into the realm of irregular polygons, where sides dance in asymmetry. Fear not, for our trusty formula adapts with grace. A pentagon, with its five capricious sides, bows to the same formula: Perimeter = Sum of side lengths. Measuring each side with precision, we let the calculator wield its magic and disclose the coveted perimeter.
Delving into Polygons’ History: Tracing Roots and Seeds
Polygons, concealing a rich history, have left their footprints in the annals of mathematics. The ancient Greeks, renowned for their geometric prowess, reveled in polygon exploration. Pythagoras, the mathematical luminary, is credited with unraveling the secrets of the Pythagorean theorem, a cornerstone in understanding right-angled polygons. Archimedes, another Greek visionary, ventured into the realm of regular polygons and calculated the area of a circle by inscribing it within a regular polygon.
Polygons in Nature: A Harmony of Form and Function
Nature, an inexhaustible source of inspiration, showcases astounding examples of polygons. Honeycombs, crafted by master architects—bees—are hexagonal marvels, maximizing storage capacity and structural integrity. Snowflakes, ephemeral masterpieces, adorn winter landscapes with intricate six-sided symmetry. These natural wonders embody the harmony between geometry and nature, whispering tales of efficiency and beauty.
How To Find The Perimeter Of A Polygon With Vertices
Conclusion: A Journey’s Epilogue
Our voyage into the world of polygons has drawn to a close, illuminating their captivating nature and revealing the secret to finding their perimeter. Armed with the formula—Perimeter = Sum of side lengths—we can confidently conquer polygons of all shapes and sizes. Remember, curiosity and exploration are the cornerstones of discovery, inspiring us to unravel the mysteries that lie hidden within geometry’s fascinating realm.